Doctoral thesis: Non-reversible parallel tempering on optimized paths

Abstract

Parallel tempering (PT) methods are a popular class of Markov chain Monte Carlo schemes used to sample complex high-dimensional probability distributions. They rely on a collection of $N$ interacting auxiliary chains targeting tempered versions of the target distribution to improve the exploration of the state-space. We provide here a new perspective on these highly parallel algorithms and their tuning by identifying and formalizing a sharp divide in the behaviour and performance of reversible versus non-reversible PT schemes.

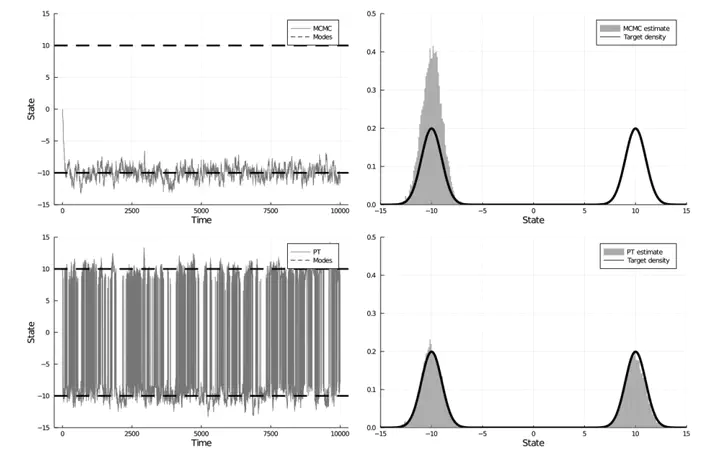
We show theoretically and empirically that a class of non-reversible PT methods dominates its reversible counterparts. These results are exploited to identify the optimal annealing schedule for non-reversible PT and to develop an iterative scheme approximating this schedule. The proposed methodology is applicable to sample from a distribution ${\pi }_1$ with respect to a reference distribution ${\pi }_0$, and to compute normalizing constants. We provide a wide range of numerical examples supporting our theoretical and methodological contributions.

The performance of non-reversible PT depends on how quickly a sample from the reference distribution makes its way to the target, which in turn depends on the particular path of annealing distributions. Traditionally PT has used only simple paths constructed from convex combinations of the reference and target log-densities; we demonstrate that this path performs poorly in the setting where the reference and target are nearly mutually singular. To address this issue, we expand the framework of PT to general families of paths, formulate the choice of a path as an optimization problem that admits tractable gradient estimates, and propose a flexible new family of spline interpolation paths for use in practice. We show that PT induces a geometry on the space of probability distributions and characterize these optimal paths as length minimizing geodesics between ${\pi }_0$ and ${\pi }_1$. Theoretical and empirical results demonstrate that our proposed methodology breaks previously-established upper-performance limits for traditional linear paths.

Finally, we identify distinct scaling limits for the non-reversible and reversible schemes, the former being a piecewise-deterministic Markov process and the latter a diffusion